Constrained low rank approximations
My research interests is mining information out of rich datasets. In particular, my work is based on the sparse approximation paradigm, where a few patterns are sought that explain a large part of the dataset. In this setting, constraints such as nonnegativity are a way to ensure these patterns are complementary descriptions of the data (e.g. they are not allowed to cancel out each other), making nonnegative approximations ``part-based'' representations of dataset. On the other hand, low-rank approximations (LRA) aim at producing simple patterns that are easily exploitable.
I often consider rather abstract models, sometimes with the goal of applying them to practical problems. Nevertheless I am mostly interested in the theory of constrained low-rank approximation itself!
A few subtopics that I have particular interest in are described below.
Semi-supervised LRA
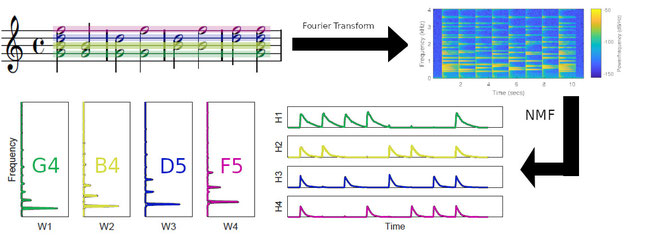
LRA are often considered for unsupervised tasks. However in several key applications (e.g. audio source separation or image processing), side information may be shipped with the data. This side information may include:
- labeled training data
- a dictionnary to build the patterns
- one or several other dataset, potentially with partial ground-truth patterns
- application-specific constraints
I am currently focussing my efforts on dictionnaries and joint distributions, both theoretical and practical aspects, through the ANR project LoRAiA.
An exemple of a dictionary of isolated note templates, recorded from a piano.
Algorithms for LRA
Most problems involving low-rank approximations and constraints are hard to solve. More precisely, given a dataset and a constrained LRA model, one should design an efficient optimization algorithm which aims at providing the best possible parameters for that model. While many efficient algorithms are today available, a few important research directions are:
- Fast algorithms in constrained or difficult settings (large, sparse or ill-conditionned data)
- Flexible algorithms which work for a large class of problems
- Algorithms with strong theoretical guaranties
- Interraction between acceleration based on hardware caracteristics (e,g, fast tensor contractions) and mathematical properties (e.g. sketching, sampling, extrapolation).
I am currently leading an Inria project for implementing fast algorithms in Tensorly, a Python library that allows to use efficient backends seamlessly.
Contact Information
CREATIS lab,